|
You can download sfrmat3 for free from http://www.i3a.org/resources/ To get Mitre SFR 1.4, please visit http://www.mitre.org/tech/mtf/ |
While based on ISO 12233, Quick MTF is not derived from any software code that implements SFR calculation in conformity with the above standard. Both Mitre SFR 1.4 and sfrmat3 are also based on ISO 12233, but they differ from each other in some respects: Mitre SFR 1.4 is designed to follow the standard as closely as possible, whereas sfrmat3 contains some improvements that make it possible to get sensible results even when the images being tested are of extremely low quality. Starting from Quick MTF 1.1, some important computing settings similar to those available in sfrmat and Mitre SFR 1.4 can be easily accessed via the menu Settings/Calculation Settings.
Y = Kr*R + Kg*G + Kb*B
For calculating the intensity, Quick MTF lets you choose either of the following two conversions:
BT.709: Kr = 0.2126; Kg = 0.7152; Kb = 0.0722;
BT.601: Kr = 0.299; Kg = 0.587; Kb = 0.114;
Mitre SFR 1.4 can handle only black-and-white images. sfrmat3 uses the conversion BT.709.
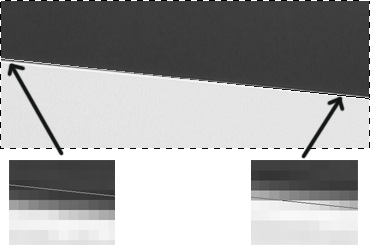
It's the first step, and the most important too. Minimizing edge detection errors is most critical for getting sensible results. The edge is usually detected by analyzing the line spread function for each pixel line. ISO 12233 mentions the use of the finite-difference schemes [-1, 0, 1] and [-1, 1]. sfrmat, Mitre SFR 1.4, and Quick MTF use the scheme [-1, 1]. Before calculating the centroids of the lines, sfrmat applies the Hamming window, but Mitre SFR 1.4 just calculates the centroids. Applying the Hamming window before calculating the centroids makes edge detection much more stable. Otherwise, edge detection errors may spoil the test results not only when "bad" images are tested, but even in very common cases (Fig. 1).
Quick MTF provides three options for edge detection:
If the "Intensity based" option is used, Quick MTF does not calculate the centroids and the LSF but only detects the edge by analyzing the intensity distribution.
On the one hand, even minor errors in finding the slope angle can lead to bad errors [1] in calculating the SFR. On the other hand, small shifts practically do not influence the calculation results. Quick MTF lets you check where exactly the edge is detected.
Severe geometric distortions or a noise level comparable to the signal level can make edge detection difficult; in such cases, you might prefer to turn off the linear regression in Quick MTF.

Fig. 1. An example of a slope calculation error when finding "pure" centroids. In this case, the results are meaningless.
At this step, the intensities for all lines are accumulated and averaged, with taking the displacement of the edge into consideration. sfrmat3 and Mitre SFR 1.4 do this operation in the same way. You can also use Quick MTF's "interpolation" option, which lets you achieve extra sub-pixel precision by linearly interpolating the intensities for each line (Fig. 2).
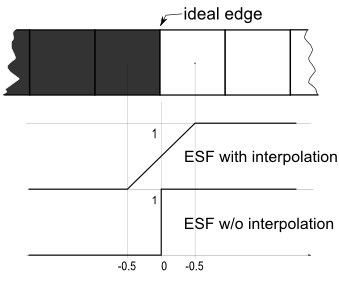
Fig. 2. Different interpretations of the ideal edge between the black pixel and the white pixel: with interpolation and without interpolation. Surely, you don't find ideal edges in real samples, but the "ideal" case nicely shows the difference.
The result obtained with interpolation looks more meaningful, because without interpolation, the SFR for any spatial frequency equals one. If correction for the difference schemes [2] is applied, the SFR will even increase with frequency, and that is contrary to the very meaning of SFR.
When binning, Quick MTF always rounds the number of cycles to a whole number; sfrmat (starting from version 3) and Mitre SFR 1.4 do the same.
Edge spread of every scan line depends on the edge's angle. Starting from version 1.02 Quick MTF applies needed corrections after binning.
The LSF is the first derivative of ESF with respect to coordinate. For calculating the derivative, Quick MTF lets you choose either of the two difference schemes: [-1, 0, 1] and [-1, 1]. sfrmat3 uses the scheme [-1, 0, 1], and Mitre SFR 1.4 uses [-1, 1].
After the LSF is calculated in Quick MTF, sfrmat, or Mitre SFR 1.4, the Hamming window is applied to the LSF. (This step is unrelated to applying the Hamming window before calculating the centroids when detecting the edge.) Quick MTF lets you turn off the Hamming window with respect to LSF.
The SFR is an absolute value of the Fourier transform of the LSF. When the transformation is done, the correction for finite differences [2] used at the step of calculating the LSF is applied to the result. Both sfrmat3 and Mitre SFR 1.4 apply the same correction.
You can easily see why such correction should be used in practice by turning it off for a while in Quick MTF and comparing the results for the difference schemes [-1, 0, 1] and [-1, 1]. The difference between the calculation results will be small but obvious. When the correction is on, the results for the two difference schemes are practically indistinguishable. So, as you can see, the correction really improves the accuracy of calculations. It is advisable to turn off the correction only if you need to do calculations similar to those implemented in the outdated sfrmat2 (or derivative software) or in any software where such correction is not implemented at all.
Oleg Kurtsev (okurtsev@quickmtf.com) © 2011
Sources: